Summary

Three weeks ago, we released ArtShield beta, which watermarks your image with the same invisible watermark that Stable Diffusion uses, in order to confuse webscraping bots on if the images are human-made or AI-generated.

Since then, we've been hard at work improving the watermark encoding success rate, as well as robustness against JPEG compression.

We consider the watermark "successful" if Stable Diffusion's decoder recognizes the watermark. This means we can not make any changes to the decoder, but we are free to change the encoder to better create a watermark that the decoder recognizes.

By improving encoding of zeros and encoding more of the watermark data into lower frequencies, we improved the watermark algorithm so that it

Quick mathematical breakdown of the watermark SD uses

To understand our improvements, here is some basic math on how Stable Diffusion's watermarker works.

A common misconception is that Stable Diffusion uses a DWT-DCT watermarking algorithm, but it does not. The invisible-watermark library contains the option to do so, but Stable Diffusion has opted only to use the discrete wavelet transform (DWT).

Here is how it works:

1. The image is converted from RGB to YUV channels.

Likely, this is done because JPEG compression operates on YUV channels instead of RGB.* Encoding the watermark in YUV channels makes it easier to create a watermark that survives the most common image compression on the web.

• Y is the luminance channel. It is how bright or dark a pixel is
• U and V are the chrominance channels. They store color data.

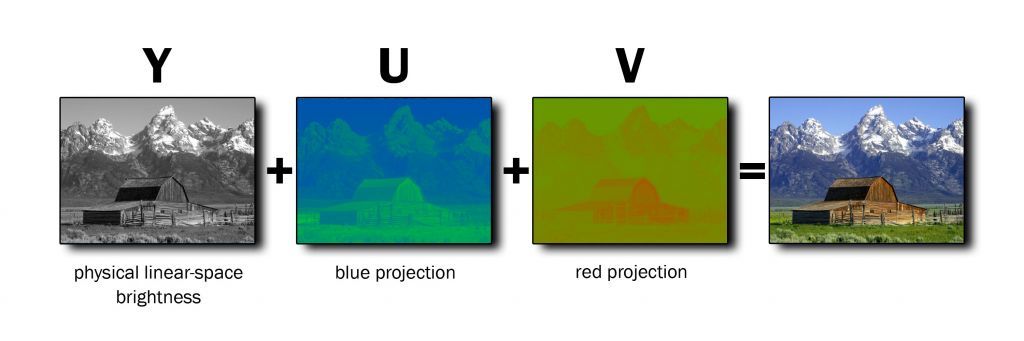
The idea is the human eye is better at distinguishing luminance than color, so the watermark gets embedded in the U chrominance channel. (They didn't choose to watermark in the V channel as well. I don't know why.)

JPEG compression also takes advantage of the fact that humans are more likely to perceive changes in the Y channel by performing more compression in the chrominance (U, V) channels. Keep this in mind for later ;)

* Technically, JPEG compression operates on the YCbCr channels, and JPEG standard is to use a modified Rec. 601 for the conversion formula. Unfortunately, the invisible-watermark library naively used OpenCV's BGR2YUV color space conversion, which can cause chrominance channels to convert with values over 255 and get clamped. This can result in vibrancy loss for some colors. We are still investigating if this is something we can solve.

2. A one level haar wavelet DWT decomposition is performed on the U channel.

That sounds more intimidating than it is. This is all that's happening:

Here is a 2x2 block of U channel pixel values, represented by S0 through S3

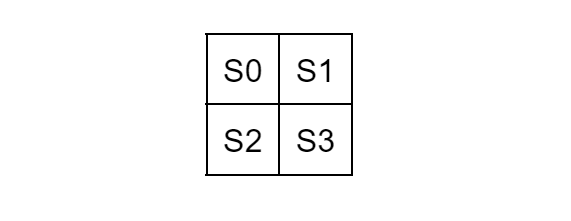
All the Haar wavelet DWT does is convert them into these easily calculatable coefficients

CA = 1/2 (S0 + S1 + S2 + S3)

CH = 1/2 (S0 - S1 + S2 - S3)

CV = 1/2 (S0 + S1 - S2 - S3)

CD = 1/2 (S0 - S1 - S2 + S3)

Each 2x2 block of pixels in the U channel gets converted into a CA, CH, CV, and CD coefficient. A 600 x 600 px image would get converted into four sets of 150 coefficients.

The original 2x2 values can be reconstructed by

S0 = 1/2 (CA + CH + CV + CD)

S1 = 1/2 (CA - CH + CV - CD)

S2 = 1/2 (CA + CH - CV - CD)

S3 = 1/2 (CA - CH - CV + CD)

Note how CA is an average of the four values. It's also called the approximation coefficient, and they it contains data on the lower frequency parts of the data. The watermark is embedded into CA coefficients.

Aside

Any time we raise CA, we raise S0 through S3 by the same amount / 2. The forward and inverse discrete Haar wavelet transforms, and raising CA are linear operations, and going back and forth between U channel space and DWT coefficient space results in no information loss.

We can therefore conclude that information loss to the watermark does not happen because of the wavelet transform. Instead, it is introduced by

• JPEG compression
• YUV/RGB conversions (This primarily affects images with lots of white and light gray pixels)
• Integer rounding (the effect is negligible)

3. The watermark is embedded into the approximation coefficients

The watermark is basically the UTF-8 letters "SDV2" as bits.

Here are the bits if you're a nerd:

01010011 01000100 01010110 00110010

Every 4x4 block of coefficients gets one bit embedded into it. If there are more 4x4 blocks than bits, then bits get encoded multiple times, giving the watermark resiliency against compression.

(You'll also notice that a 4x4 block of coefficients corresponds to an 8x8 block of pixels, which happens to be the block size that JPEG quantization operates on.)

Here's an example visualization of U channel 4x4 approximation coefficients for a small upper left corner of this image:

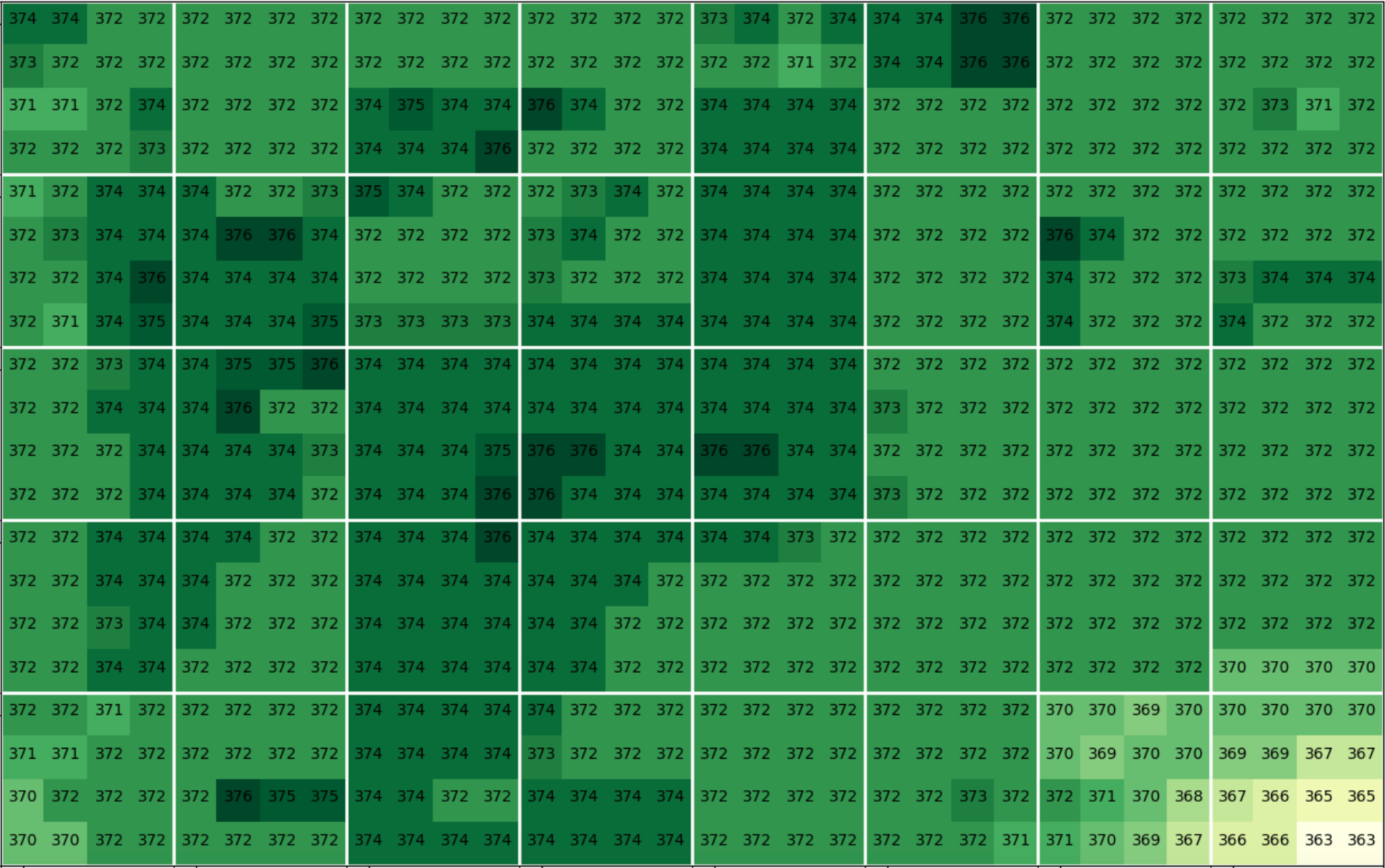
SD's watermarker finds the highest valued coefficient in each block, rounds it down to CA // 36, then adds either

• 9 to embed bit 0
• 27 to embed bit 1

Effectively, the 2x2 block of pixels with the highest average U chrominance gets to store a bit of the watermark.

4. That's it.

The image is then converted from coefficients back to pixel values, and then back to RGB.

5. The decoder

The decoder converts the U channel back into coefficients, and then lets each 4x4 block take a vote on what they were encoded with.

• The 1st block votes on the 1st bit of the watermark. The 2nd block votes on the 2nd bit, and so on.
• The 33rd block votes on the 1st bit, the 34th on the 2nd bit, and so on. (If you're confused, remember that the watermark is only 32 bits.)
• All the blocks that correspond to the first bit take a vote. Do they think they were encoded with a 0 or with a 1? Collectively, they decide the first bit of the watermark.
• The same voting process happens for the 2nd bit, and so on.
• When all 32 bits are tallied, the bits are decoded back into UTF-8 to see if they form the watermark "SDV2"

Now that you have the math - here’s what we improved:

1. When encoding a 0 bit, we take into account surrounding coefficients

The decoder look at the highest valued CA coefficient in each block, and sees if it is encoded with 0 or 1.

It does this by seeing is

(CA % 36) / 36

closer to 0 or 1?

However, what happens when SD's watermarker lowers the coefficient to embed a 0, but the surrounding coefficient are higher, and read as 1's? The block will still decode as 1.

Let's go through a more concrete example:

Here's an example unwatermarked 4x4 block:

The SD watermarker will look for the highest coefficient in the block, and to encode a 0, it will set it to 31 // 36 + 9 = 9

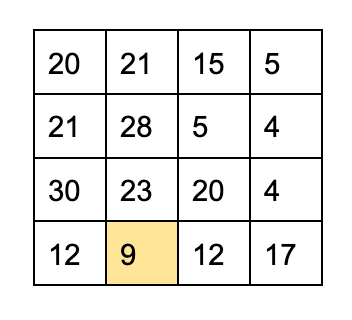
However, when the decoder looks at this, it looks for the highest. In this block, that's 30, not 9.

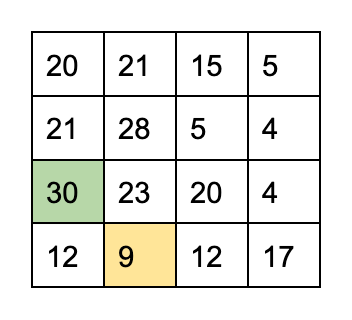
(30 % 36) / 36 = 30 / 36 = 5/6

5/6 is closer to 1 instead of 0. Even though the watermarker tried to encode a 0 in this block, it will decode as a 1.

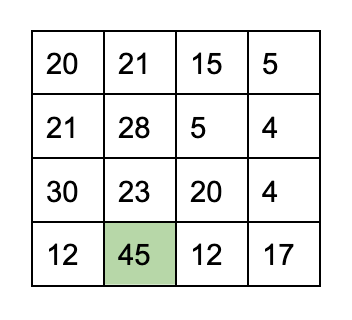
Our first change was, we encode 0s in a way that the highest coefficient in a block will decode to 0. In this example, we will instead increase 36 to 45.

(45 % 36) / 36 = 9 / 36 = 1/4

1/4 is closer to 0 than 1, so now this block will properly decode as 0.

2. We embed a gradient into the surrounding coefficients

The key thing to understand about JPEG compression is that lower-frequency data is much more likely to survive JPEG compression than higher-frequency data.

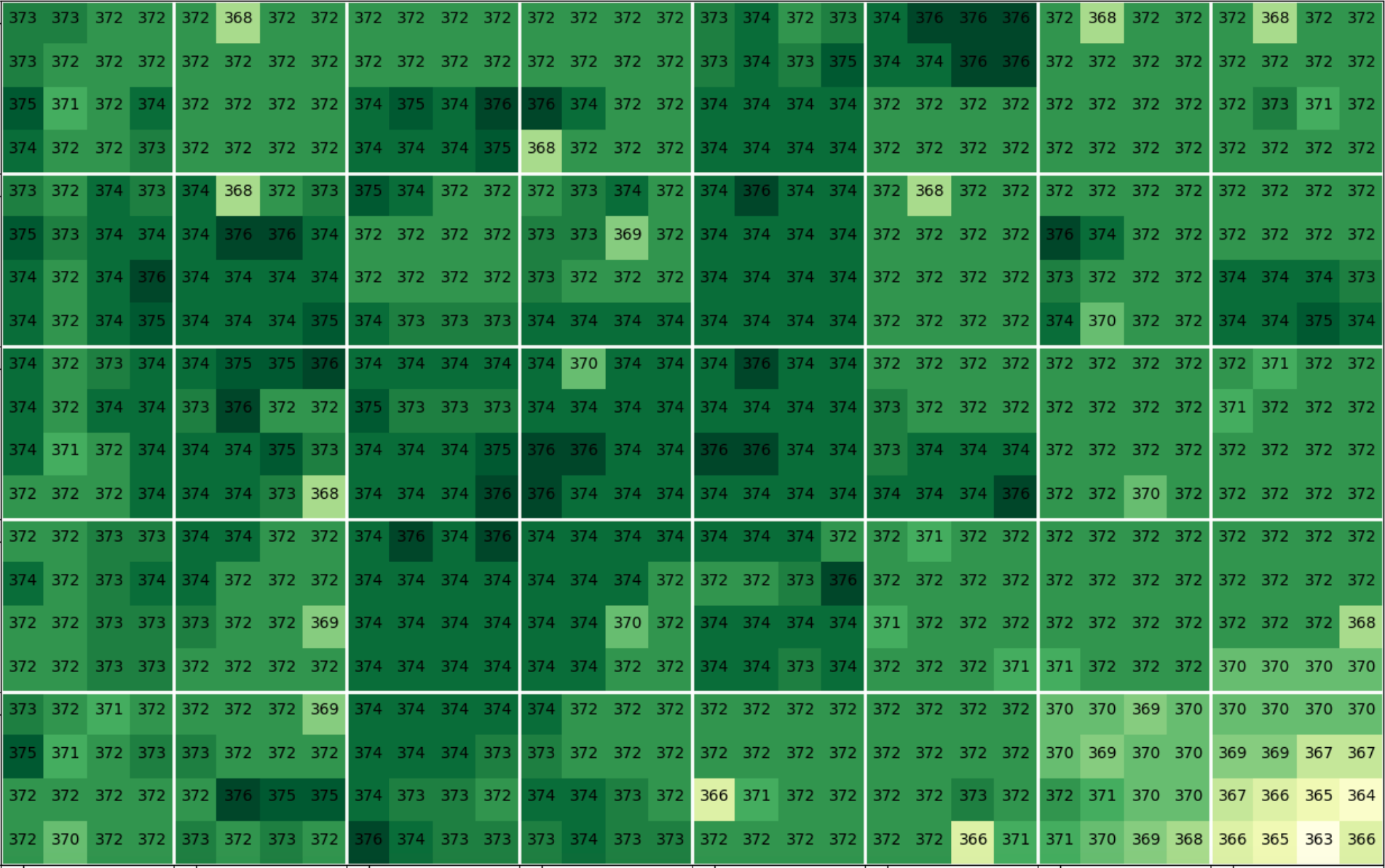
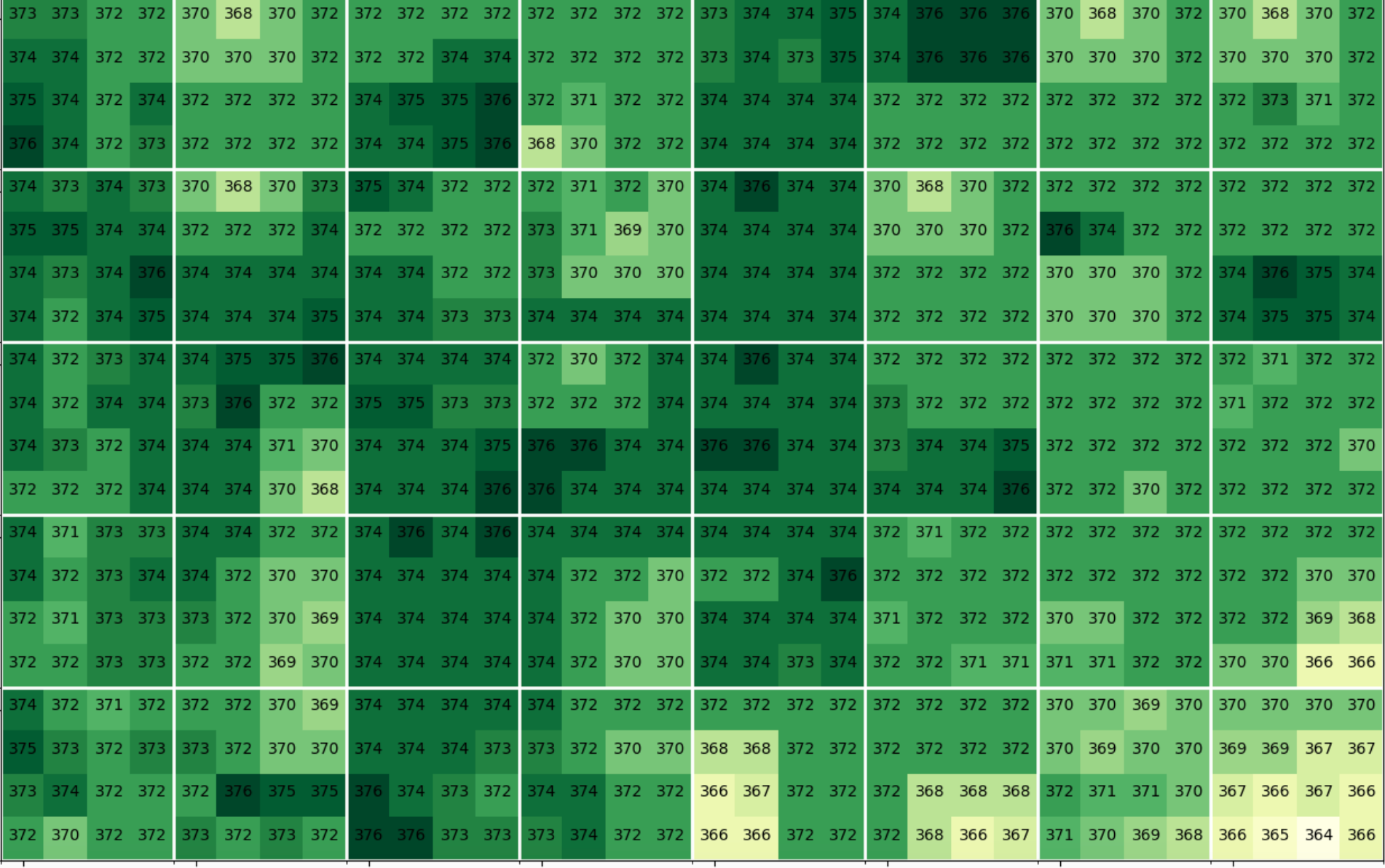
By embedding a gradient into the surrounding coefficients, instead of just our target coefficient, we can put more watermark data into lower frequencies, making it more robust against compression.

Without gradient:

With gradient:

Performance improvement

Un-watermarkable background colors

SD's watermarker struggles to embed single-color background. This is related to how it can struggle to encode 0 bits if the surrounding coefficients are higher.

We tested on solid-color images of these 213 colors curated by lunohodovtest by embedding the watermark and seeing if we could detect it.

With SD's watermarker, 115/213 colors encoded successfully.

With our improved watermarker, 207/213 colors encoded successfully.

You can see here the 6 colors we could not embed. We know these issues are related to data loss during YUV/RGB conversion, and we are still considering solutions.

Jpeg compression

We compiled a list of 100 public domain images to test against and tested three watermarking algorithms on each of them

1. SD's original watermark
2. Our watermark with improved encoding of 0 bits
3. Our watermark with improved encoding of 0 bits, and gradient embedding

We save the watermark-encoded image as an uncompressed PNG and test if we can detect the watermark on it to determine if the image was successfully encoded. (See Uncompressed column)

Successfully encoded images are then saved as a JPEG compressed with 90, 80, and 70 quality, and 4:4:4, 4:2:2*, and 4:2:0 chroma subsampling. Finally, these compressed images are tested to see if the decoder can detect the watermark. (See JPEG columns)

* 4:2:2 chroma subsampling is not common in web compression

You can see our results here:

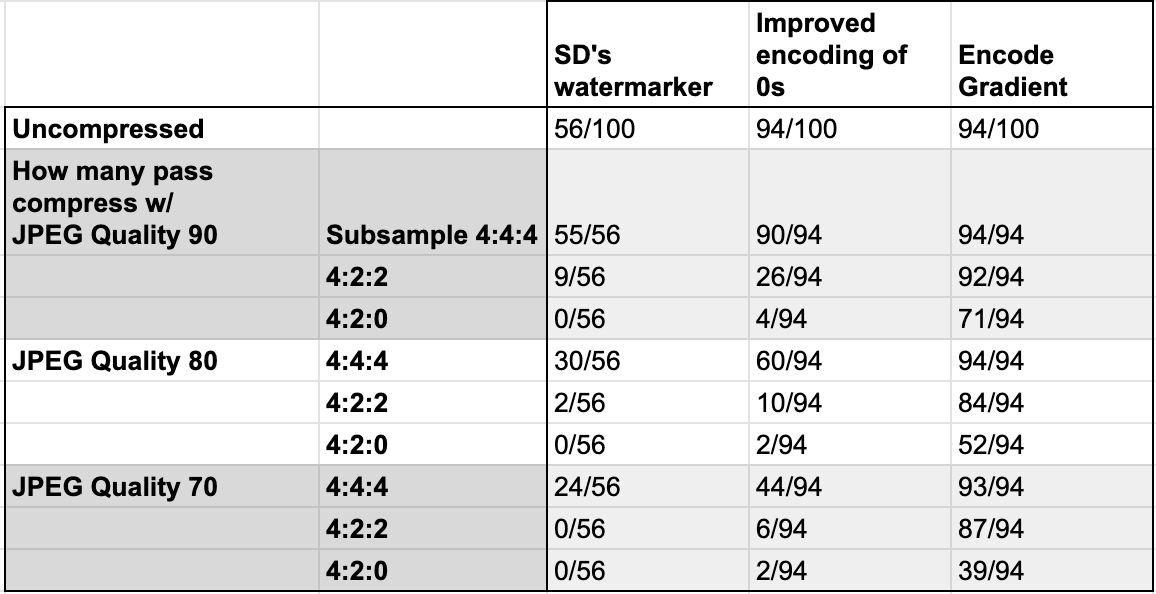
Our improvements in watermarking allowed us to successfully watermark 94/100 images, compared to SD's 56/100. (The six images we could not watermark all have primarily white or near-white backgrounds.)

For almost all non-insignificant amounts of JPEG compression, our improved gradient watermark survives much better than SD's original watermark.

By looking at these results, you can see that chroma subsampling is particularly hard for the watermark to survive

Chroma subsampling operates on the U and V channels, and it represents multiple pixels with the same U and V value. This is lossy, and can remove the watermark from a block by overwriting the watermarked CA coefficient's value.

In cases of 4:2:0 subsampling, SD's watermark almost never survives it. While our gradient-encoded watermark doesn't survive all instances, it still performs significantly better.

Although we have the option to even further improve robustness, we decided not to because it came with too many noticeable changes to the watermarked images.

Aside: At first glance, it may look like our performance against 90% quality, 4:4:4 subsampling is worse than the default watermarker. However all 55 images w/ the old watermark that survived the compression also survived with our new watermark.

As mentioned, we have the option to even further improve robustness, but decided against it in favor of image fidelity. For the 38 newly-watermarkable images, they seem to be more fragile at because we made this tradeoff.

Jpeg robustness of smaller images

We also resized each of the 100 original images to half their original width and height, watermarked them, and then tested them again for robustness against JPEG compression. Here are our results:

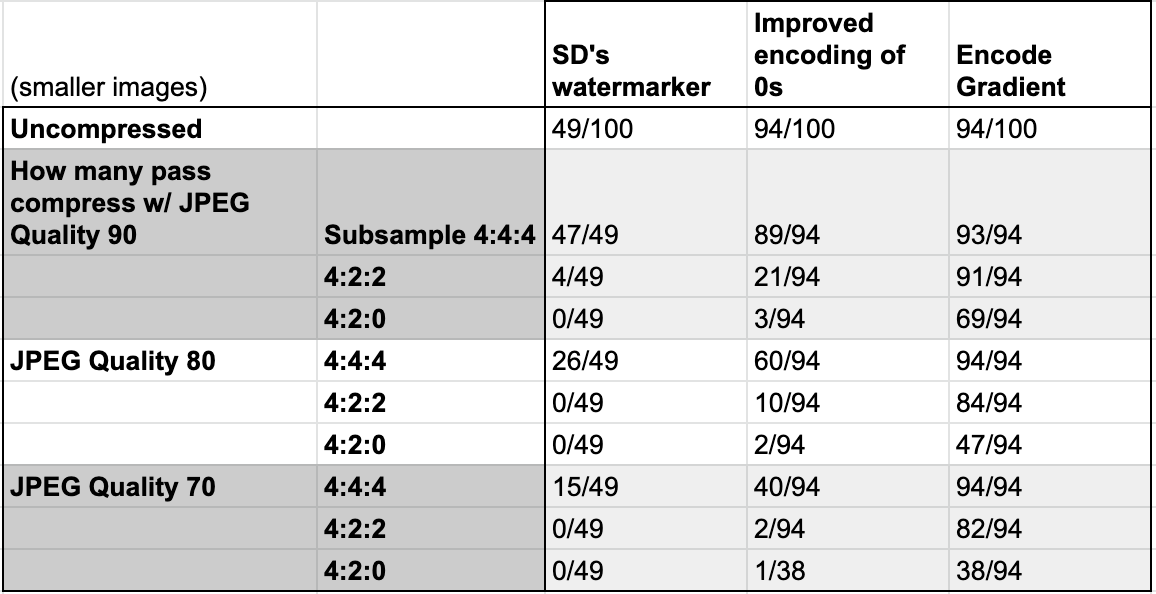
All images that were watermarkable are still watermarkable in their smaller size.

Additionally, we observe a less than 5% loss in robustness against JPEG compression in smaller images. You can see in the chart there is only a small drop in the number of images with watermarks that survive compression.

Watermark invisibleness comparison

We selected a few images to demonstrate what artwork looks like after the watermarks are applied

Farm near Duivendrecht by Piet Mondrian

Paris Street; Rainy Day by Gustave Caillebotte

Cranes on Branch of Snowladen Pine by Katsushika Hokusai

What updates we will make to ArtShield

ArtShield will now return two watermarked images.

1. The watermark with improved encoding of 0 bits
2. The robust watermark with improved encoding of 0 bits, and gradient embedding

The first image is intended to be used where the artist has more control over image quality. This may include personal portfolios or personal websites.

The second image is more robust against compression, at the cost of more changes made to the image. It should be used where the artist has less control over image quality. This may include Etsy, Twitter, or Shopify.

Additional Notes/Next Steps

Address how watermark cannot be embedded into white pixels

We understand many artists have art with lots of white pixels, so this is an important use case.

When embedded on white pixels, the watermark is destroyed by clamping during YUV/RGB conversion.

Possible solutions are:

• We can turn embedded pixels off-white
• If enough of the image is non-white, the watermark is still embeddable, but does not hold up well to compression
• We can hide a barely-transparent pixel in the PNG alpha channel. This can force some platforms to store the image as PNG and not perform JPEG compression on it. If we don't have to worry about watermark data loss during compression, then we won't need to successfully embed in as many coefficients

Probabilistic calculation of watermark likelihood

Currently, we call the watermark a success if we can perfectly decode the bits for "SDV2" from the image. However, even if we only manage to decode 30 out of 32 bits, we can and say with >99.99% certainty the image was watermarked (Assuming equal likelihood of 0 and 1 bits)

We could even take into account the votes for each bit, instead of just the final tallied result.

Considering the poor performance of the existing SD watermarker, it's not unreasonable to expect any bots looking for it will use a better criteria that takes into account the likelihood of watermark existence, instead of a simple binary yes or no watermark. If we could provide an improved decoder for the calculation, we can push for a higher adoption rate of the probabilistic decoder too.

The watermark is not resilient to cropping, rotation, or resizing.

It's important to note that a core shortcoming of this watermark is that it is not resilient to resizing and cropping whatsoever. There are watermarking algorithms that are resilient.

If we can make a humble suggestion, the industry should explore using one that is more robust to common image functions like resizing and cropping.